CS173: Intro to Computer Science - Searching and Sorting

Activity Goals

The goals of this activity are:
  1. To be able to search a list for a desired item.
  2. To be able to sort a list using the iterative sorting algorithms Bubble Sort, Insertion Sort, and Selection Sort

Supplemental Reading

Feel free to visit these resources for supplemental background reading material.

The Activity

Directions

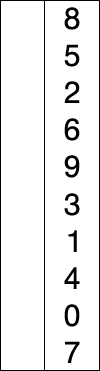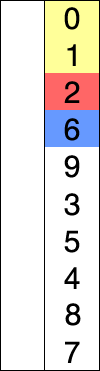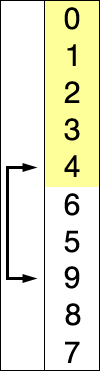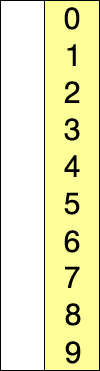
Consider the activity models and answer the questions provided. First reflect on these questions on your own briefly, before discussing and comparing your thoughts with your group. Appoint one member of your group to take notes for the group, and appoint another member to discuss your findings with the class. After class, think about the questions in the reflective prompt and respond to those individually. Report out on areas of disagreement or items for which you and your group identified alternative approaches. Write down and report out questions you encountered along the way for group discussion.

Model 1: Searching

6
7
10
3
4
2
1
8
5
9

Questions

  1. What steps are required to find the index of an item in the array (say, the number 2)?
  2. Write Java-like pseudocode to implement a function to locate a value k in an array A.
  3. How many iterations are required through the loop to find item 6? How about item 9?
  4. How many iterations are required through the loop to find the last item in a list of size N?

Model 2: Insertion Sort


Insertion-sort-example-300px
Consider the array defined in this example: [ 4, 3, 2, 10, 12, 1, 5, 6 ]

Questions

  1. Notice that the pseudocode for InsertionSort begins with i = 1, not 0. Why might this be?
  2. After each iteration of the loop, how many elements of A are in sorted order? Where are these elements located?
  3. How many are not yet in sorted order, and where are these located?
  4. If the inner j for loop goes all the way to index 0 without finding the key, what do we know about the value we’re inserting in this step?
  5. What is the purpose of the line A[j+1] = A[j] inside the inner for loop?
  6. Describe the execution of this algorithm in your own words.
  7. Enter the code for Insertion Sort into the Java Visualizer and execute it step-by-step.
  8. How many steps are required to execute this code on an array of size 10? In other words, how many times is the code inside the inner loop executed? How does this count relate to the size of the array?

Model 3: Selection Sort

The benefits of a Binary Search algorithm required that we use a sorted list. Given an unsorted array, we can sort it with an algorithm.

Selection Sort is similar to Insertion Sort, except that it searches the array for the smallest item, and inserts it on the left position. It continues doing this, except that in step 2, it searches for the smallest item in the sub-array that starts at index 1 (instead of 0, since that was the smallest element from the last step, and now we’re looking for the "second smallest element"). It continues to insert the "next smallest element" into the left position of the array, to the right of the ones it has inserted before. So, the "second smallest" element goes in the "second position" from the left, and the "third smallest element" goes in the "third position from the left," and so on. It "Selects" the smallest element that has yet to be sorted, and places it into the proper position.
Selection-Sort-Animation

Questions

  1. After each iteration of Selection Sort, how many elements are in sorted order, and where are they located?
  2. After each iteration, how many elements are still unsorted, and where are they located?
  3. What is the pseudocode to find the smallest element in an array?
  4. Modify this "smallest element finder" pseudocode into a function that finds the smallest element in an array, but with a parameter to indicate what positions to start and stop searching (i.e., the starting and stopping indices).
  5. What is the pseudocode to swap two elements in an array, given their indices?
  6. Enter the code for Selection Sort into the Java Visualizer and execute it step-by-step.

Model 4: Bubble Sort

Bubble-sort-example-300px

Questions

  1. Describe the execution of Bubble Sort in your own words.

Submission

Submit your answers to the questions using the Collaborative Spaces section of OneNote. You can add a page with your name and your group members' names, and today's date, as the title. Under the appropriate section (i.e., "Class Notes", "Collaborative Spaces", "Reflective Prompts") that you can select on the left side of the screen, you can click "Add Page" on the right side. You can answer any reflective prompt questions in the Reflective Journal section of your OneNote Classroom personal section.

For Additional Practice

Feel free to visit these resources for additional practice exercises.