CS173: Intro to Computer Science - Recursion and Merge Sort

Activity Goals

The goals of this activity are:
  1. To apply recursion to the sorting problem using Merge Sort and Quicksort
  2. To identify a recursive base case
  3. To implement recursive algorithms
  4. To be able to apply recursion to the search problem.

Supplemental Reading

Feel free to visit these resources for supplemental background reading material.

The Activity

Directions

Consider the activity models and answer the questions provided. First reflect on these questions on your own briefly, before discussing and comparing your thoughts with your group. Appoint one member of your group to take notes for the group, and appoint another member to discuss your findings with the class. After class, think about the questions in the reflective prompt and respond to those individually. Report out on areas of disagreement or items for which you and your group identified alternative approaches. Write down and report out questions you encountered along the way for group discussion.

Model 1: Recursive Algorithms


Diagram of Fibonacci Recursive Calls

Questions

  1. Notice that the algorithm "starts over" on a smaller part of the array after each guess. This is a hallmark of a "recursive algorithm." They are like loops. Do you think this approach requires more or less code to write than a non-recursive version? Why or why not?
  2. How many times did this algorithm compute fib(2)?

Model 2: Searching with Recursion

1
2
3
4
5
6
7
8
9
10

Questions

  1. Suppose you are playing the "high-low" game, in which you have to guess a number, and are told that the correct value is higher or lower than your guess. What would be the best first guess, if you knew the value was between 1 and 10?
  2. How do you know that a value will definitely be found in the right half of the array? How about on the left half of the array?
  3. Now, suppose you are playing the same "high-low" game, but instead of knowing the range of values you’re looking for, you know how big the array is that you’re searching. You are still told whether your value is higher or lower than your guess. Which element would you pick for your guess? In mathematics, this element or value is known as the ______ of the list?
  4. Try searching for the value 8. Write down which indices of the array you are searching within (initially 0 through 9), and the index of your guess, at each step of the search, until you find the value 8. How many guesses were required? How many guesses would have been required if the list was not sorted?

Model 3: Efficient Sorting with Recursion - Merge Sort

Merge Sort views the problem of sorting as a recursive one: sorting a large list is the same as breaking the list in half, sorting each of those, and then "merging" them together as if they were a deck of cards being shuffled.

Questions

  1. What would the base case of Merge Sort be? When might you stop splitting the array in half?
  2. Given two sorted arrays, how would you go about merging them together?
  3. Write the pseudocde for Merge Sort - there are exactly 3 steps (recursively calling the left half, followed by the right half, followed by a call to the merge step completed above).
  4. What indices would you provide to sort the left half, right half, and merge steps at each recursive iteration?
  5. Enter the code for Merge Sort into the Java Visualizer and execute it step-by-step.

Model 4: Efficient Sorting with Recursion - Quicksort

Quick Sort views the problem of sorting as a recursive one: sorting a large list is the same as sorting two smaller lists. The problem gets smaller at each step as long as we learn the correct sorted position of one item at every step (just like with Selection Sort and Insertion Sort).
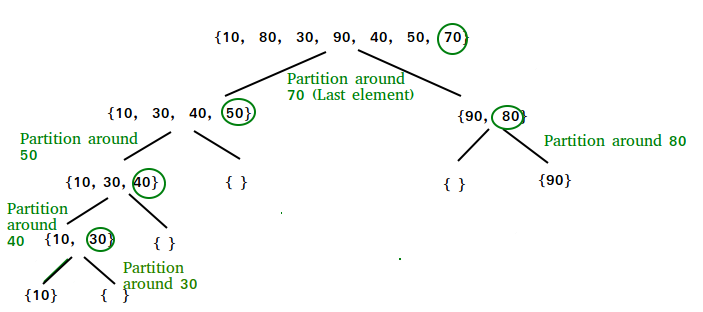
Quicksort Diagram from geeksforgeeks

Questions

  1. The array is broken into two sub-problems at each step. What do you notice about the elements in the left sub-problem and the elements in the right sub-problem? How are they being "partitioned" into the two sub-arrays?
  2. Notice that the problems aren’t always divided exactly into halves. That’s because the algorithm is "partitioning" the values according to the last value of the array. What would be the ideal choice of an element to "partition" around (this element is known as the "pivot")?
  3. The "partition" results in two sub-problems, with sub-arrays that include all the elements from the main problem, except for one. Which element is left out, and why?
  4. After each recursive iteration of Quick Sort, how many elements are placed into their correct position? Where are they located?
  5. Enter the code for Quick Sort into the Java Visualizer and execute it step-by-step.

Reflective Journal Prompt

  1. How might you improve upon (reduce) the number of calls to fib(2) in the Fibonacci example?

Submission

Submit your answers to the questions using the Collaborative Spaces section of OneNote. You can add a page with your name and your group members' names, and today's date, as the title. Under the appropriate section (i.e., "Class Notes", "Collaborative Spaces", "Reflective Prompts") that you can select on the left side of the screen, you can click "Add Page" on the right side. You can answer any reflective prompt questions in the Reflective Journal section of your OneNote Classroom personal section.

For Additional Practice

Feel free to visit these resources for additional practice exercises.